완전탐색 문제를 풀다가 순열과 조합 유형이 자주 나와서 계속 풀어보고 있다. nCm을 구하는 것이 문제이다.
1. 문제
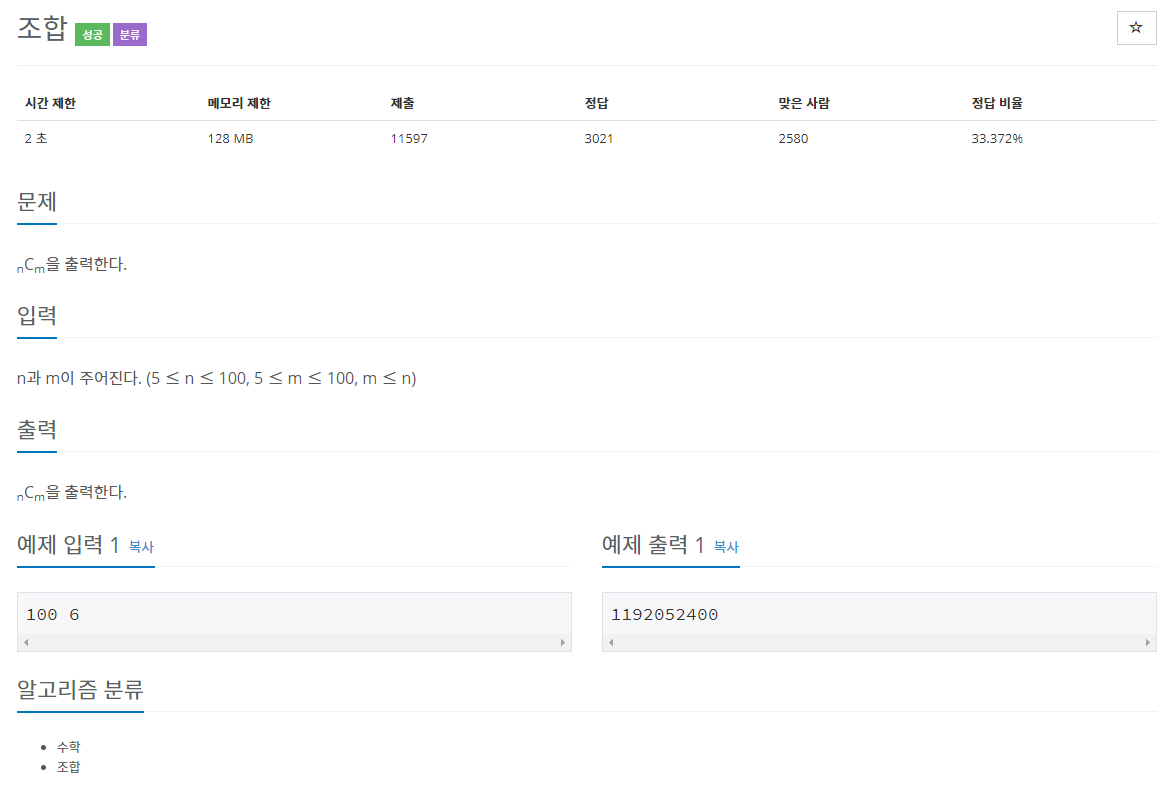
2. 풀이 과정
2.1 재귀를 통한 접근
첫번째 접근 방법은 고등학교 때 배운 파스칼의 삼각형을 떠올려, 재귀를 이용한 방법으로 풀어보았다. 코드는 아래와 같다.
import java.util.Scanner;
public class Main {
public static long paskal(int n, int m){
if(m == 0 || n == m){
return 1;
}
return paskal(n-1,m-1) + paskal(n-1,m);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
long num1 = paskal(n,m);
System.out.println(num1);
}
}하지만 제출 결과 시간 초과가 났다. 생각해보면 당연한 결과 였다. 각각의 재귀 함수가 똑같은 연산을 계속 반복하니까 시간이 오래걸릴 수 밖에 없다.
2.2 다이나믹 프로그래밍(DP)를 이용한 접근
두번째로 생각한 방법은 다이나믹 프로그래밍이다. 재귀 함수에서 동일한 계산을 계속 해주기 때문에 2차원 배열을 하나 선언해서 처음부터 값을 넣는다면 그렇게 오래 걸리지 않는다. 여기서 하나 더 고생했던 것은 배열을 처음에 long으로 선언했는데 계속 답이 틀려서 BigInteger로 수정하니까 정답으로 처리가 되었다.
long 타입으로 표현할 수 있는 범위는 "-92233720368547758078~ 9223372036854775807"까지 표현할 수 있다. 이를 넘는 숫자를 처리할 때는 BigInteger를 사용한다.
import java.math.BigInteger;
import java.util.Scanner;
public class Main {
public static BigInteger dpCombi[][];
public static void setDpCombination(int n, int m){
for(int i=1;i<=n;i++){
for(int j=0;j<=i;j++){
if(j == 0 || j==i)
dpCombi[i][j] = new BigInteger("1");
else
dpCombi[i][j] = dpCombi[i-1][j-1].add(dpCombi[i-1][j]);
}
}
}
public static void main(String[] args) throws Exception{
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
dpCombi = new BigInteger[1001][1001];
setDpCombination(n, m);
System.out.println(dpCombi[n][m]);
}
}조합의 개수를 구해야하는 경우에는 이렇게 다이나믹 프로그래밍을 활용하면 금방 풀 수 있다.
'Algorithm' 카테고리의 다른 글
| [알고리즘] 프로그래머스-소수찾기 (완전탐색) (0) | 2020.07.20 |
|---|---|
| 백준 10974번 모든 순열 (java) (0) | 2020.07.20 |
| [BAEKJOON] 2004번: 조합 0의 개수 (Java) (1) | 2020.07.12 |
| [Algorithm] 조합 코드 구현 (Java) (4) | 2020.07.12 |
| [알고리즘] 프로그래머스-모의고사 (완전탐색) (0) | 2020.06.16 |



